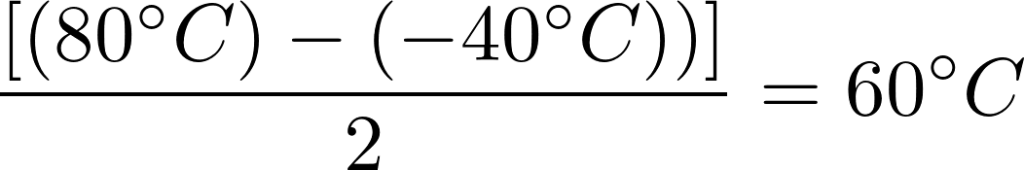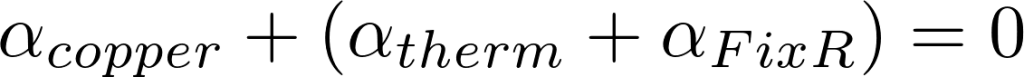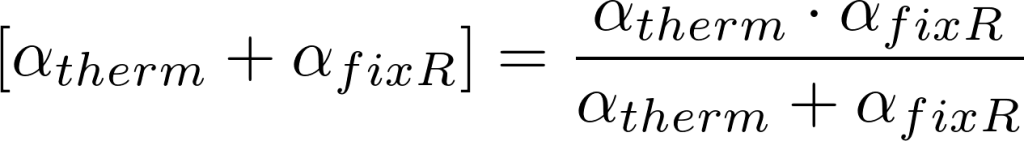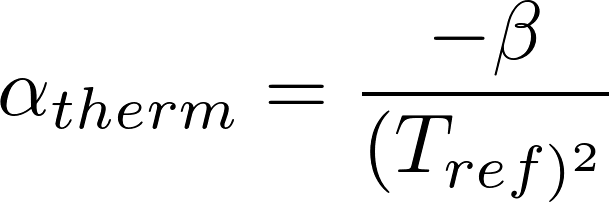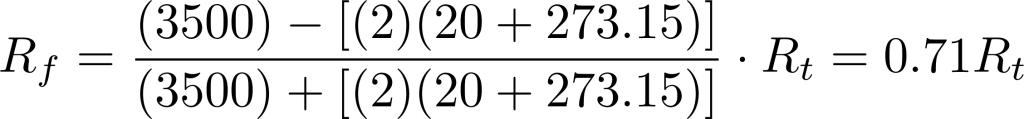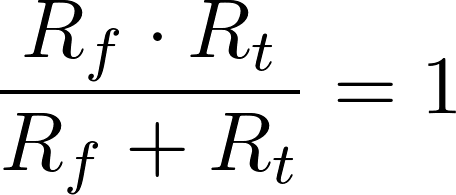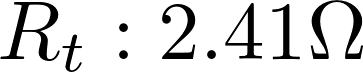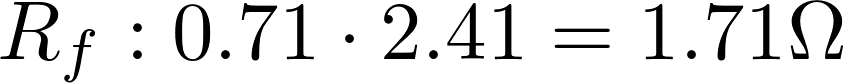基于热敏电阻的温度补偿
简单和低成本是热敏电阻的关键优势。甲负温度系数(NTC)热敏电阻,例如,提供了一种基于环境温度可变电阻。该电阻遵循在-40至+ 80℃的期望温度范围内的相对线性响应[工业用~120]。
在传统的监控系统中,这允许CPU执行简单的表查找以确定温度并将其与阈值进行比较以查看是否需要冷却。CPU还可以调节螺线管或LCD的电流,但这需要CPU周期以及额外的电路来将此功能扩展到CPU。
更简单的方法是将热敏电阻集成到独立的温度补偿电路中。热敏电阻与固定电阻串联。通过这种方式,热敏电阻的变化电阻可以自动调节流过螺线管,LCD或其他温度敏感元件的电流量,而无需CPU参与。
螺线管的铜线圈随温度升高呈现正温度系数。由于NTC热敏电阻通常具有-3.3%/℃至-4.9%°/℃的温度系数范围,因此使用温度系数为440ppm的固定并联电阻器将温度系数降低到可用的极限。例如,铜在-40℃至+ 80℃的温度范围内具有0.4%/℃的温度系数。线圈电阻变化为80±20欧姆(见表1),具有以下特性。此外,线圈承载0.85安培的电流,这也将通过热敏电阻导致自热:
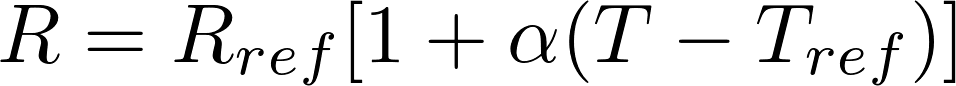
方程(1)
哪里:
- R是温度T下的导体电阻
- R ref是参考温度T ref下的导体电阻(假设为20°C)
- α是导体材料的电阻温度系数
- T是导体材料的工作温度,单位为摄氏度
- T ref是指定导体材料的α的参考温度,也表示中点温度
- 在方程(1)中代入铜螺线管的温度系数α为每°C .4167%
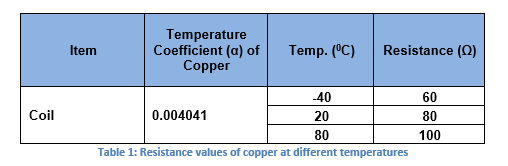
使用表1中的值,考虑的参考值为:
T ref = 20°C且R ref =80Ω
考虑的系统具有与这对线圈串联的电阻。根据设计,该串联电阻的值应为97.15Ω,以使系统按预期工作(参见下面的图1)。请注意,总电阻为177.15Ω。
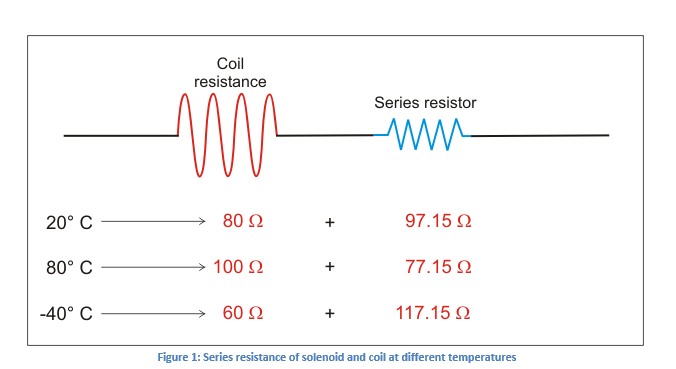
目的是找到一个温度补偿电路,它可以抵消螺线管的正温度效应和串联电阻。为了减小阻力波动,理想的范围是使曲线在其中心变平。
由于螺线管和LCD的响应性在所需温度范围内足够线性,因此可以使用标准线性化方程。该等式基本上是固定电阻器与 特定温度下的热敏电阻器的电阻之比(即,通常在最低和最高所需工作温度的中点)。此外,精度对于该电路并不重要。它只需要能够在电磁阀冷却时增加大约理想的电流量,并在热时适当降低电流。
考虑一个由热敏电阻组成的线性化电路(图2),其中:
- R c是包括串联电阻的线圈电阻
- R t是热敏电阻
- R f是固定电阻
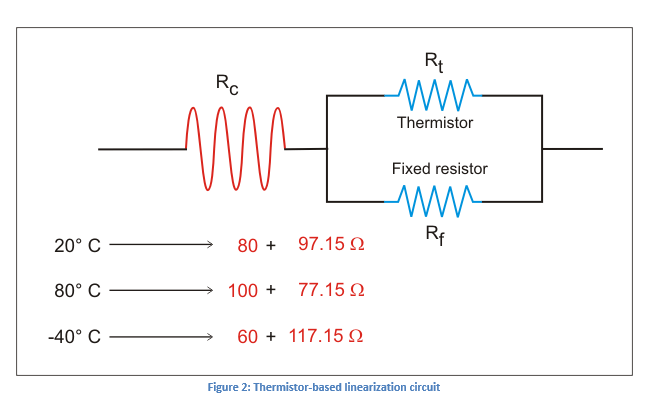
上述电路的总电阻为177.15 + K,其中
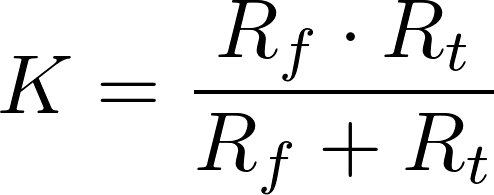
方程(2)
注意线圈(串联)电阻为177.15-K
。用于使热敏电阻曲线变平的线性化方程如下:
固定电阻值R 电阻 = R f
热敏电阻电阻值R 热敏电阻 = R t
因此,线性化方程:
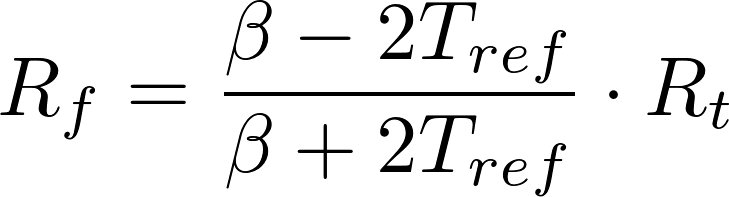
方程(3)
哪里:
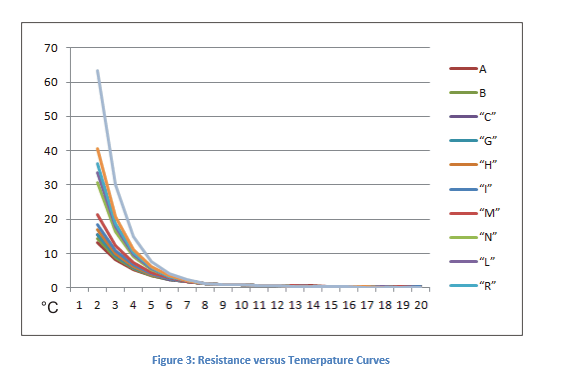
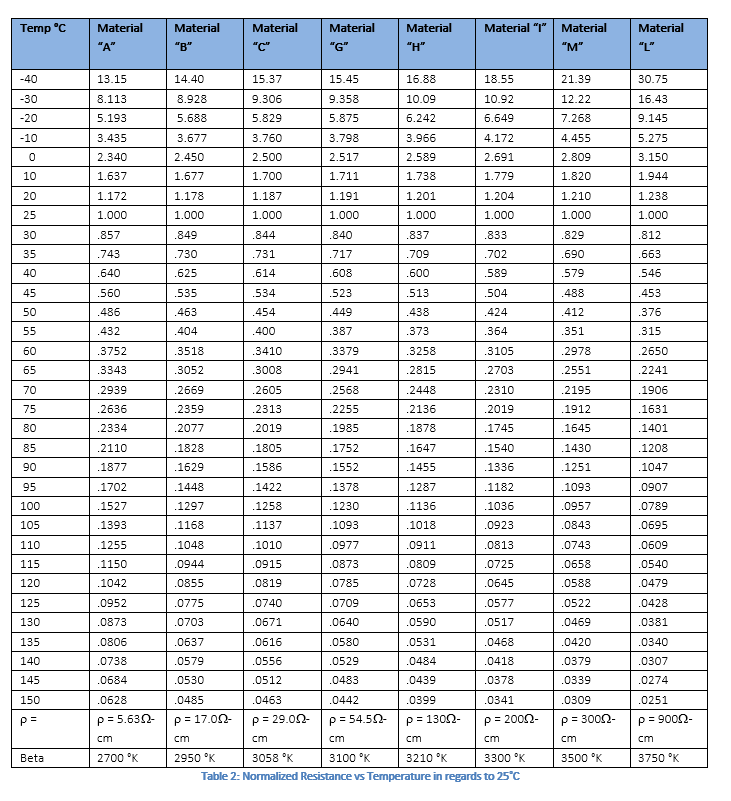
β=材料常数=在我们的例子中= 3500°K(考虑曲线M,见图3)
T ref,中点温度计算如下: